HUKUM BERNOULLI
Persamaan dasar dalam hidrodinamika telah dapat dirintis dan dirumuskan oleh Bernoulli secara baik, sehingga dapat dimanfaatkan untuk menjelaskan gejala fisis yang berhubungan dengan dengan aliran air. Persamaan dasar tersebut disebut sebagai persamaan Bernoulli atau teorema Bernoulli, yakni suatu persamaan yang menjelaskan berbagai hal yang berkaitan dengan kecepatan, tinggi permukaan zat cair dan tekanannya. Persamaan yang telah dihasilkan oleh Bernoulli tersebut juga dapat disebut sebagai Hukum Bernoulli, yakni suatu hukum yang dapat digunakan untuk menjelaskan gejala yang berhubungan dengan gerakan zat alir melalui suatu penampang pipa. Hukum tersebut diturunkan dari Hukum Newton dengan berpangkal tolak pada teorema kerja-tenaga aliran zat cair dengan beberapa persyaratan antara lain aliran yang terjadi merupakan aliran steady (mantap, tunak), tak berolak (laminier, garis alir streamline), tidak kental dan tidak termampatkan. Persamaan dinyatakan dalam Hukum Bernoulli tersebut melibatkan hubungan berbagai besaran fisis dalam fluida, yakni kecepatan aliran yang memiliki satu garis arus, tinggi permukaan air yang mengalir, dan tekanannya. Bentuk hubungan yang dapat dijelaskan melalui besaran tersebut adalah besaran usaha tenaga pada zat cair.
Selanjutnya apabila pengkajian hukum ini berpangkal tolak pada hukum kekekalan massa seperti yang telah disajikan pada bab terdahulu, dengan menggunakan persyaratan seperti yang telah disajikan di bagian depan maka dalam aliran ini hukum kekekalan massa tersebut lebih mengacu pada hukum kekekalan flux massa. Oleh sebab itu dalam tabung aliran semua partikel zat cair yang lewat melalui pipa/tabung yang memiliki luas penampang tertentu diandaikan memiliki kecepatan pengaliran di satu titik adalah sama pada garis aliran yang sama. Namun demikian pada titik-titik lainnya dapat memiliki kecepatan yang berbeda.
Selanjutnya untuk menurunkan persamaan yang menyatakan Hukum Bernoulli tersebut dapat dikemukakan dengan gambar sebagai berikut.

Gambar 13. Gerak sebagian fluida dalam penurunan persamaan Bernoulli
Keterangan gambar:
1. h1 dan h2 masing-masing adalah tinggi titik tertentu zat cair dalam tabung/pipa bagian kiri dan bagian kanan.
2. v1 dan v2 adalah kecepatan aliran pada titik tertentu sari suatu zat cair kiri dan kanan.
3. A1 dan A2 adalah luas penampang pipa bagian dalam yang dialiri zat cair sebelah kiri dan sebelah kanan.
4. P1 dan P2 adalah tekanan pada zat cair tersebuut dari berturut-turut dari bagian kiri dan bagian kanan.
Gambar di bagian depan merupakan aliran zat cair melalui pipa yang berbeda luas penampangnya dengan tekanan yang berbeda dan terletak pada ketinggian yang berbeda hingga kecepatan pengalirannya juga berbeda. Dalam aliran tersebut diandaikan zat cair tidak termampatkan, alirannya mantap sehingga garis alir merupakan garis yang streamline, demikian pula banyaknya volume yang dapat mengalir tiap satuan waktu dari pipa sebelah kiri dan kanan adalah sama.
Dari gambar, dapat dikemukakan bahwa zat cair pada semua titik akan mendapatkan tekanan. Hal ini berarti pada kedua permukaan yang kita tinjau (lihat gambar yang diarsir) akan bekerja gaya yang arahnya ke dalam. Jika bagian ini bergerak dari posisi pertama menuju bagian kedua, gaya yang bekerja pada permukaan pertama akan melakukan usaha terhadap unsur yang ditinjau tadi sedangkan bagan tersebut akan melakukan usaha terhadap gaya yang bekerja pada permukaan sebelah kanan. Selisih antara kedua besaran usaha tersebut sama dengan perubahan energi gerak ditambah energi potensial dari bagian tersebut. Selisih kedua besaran energi tersebut disebut sebagai energi netto. Secara matematis dapat dinyatakan sebagai berikut:
p1 ∆1 ∆11 – p2 ∆2 ∆12 = (½ mv21 – ½ mv22) + (mgh2 – mgh1)
A ∆ 1 = v
p1 v1 – p2 v2 = ½ m (v21 – v22) + mg (h2 – h1)
Pada hal v = m/ρ, maka persamaan dapat diubah menjadi:
p1 (m/ρ) – p2 (m/ρ) = ½ m (v21 – v22) + mg (h2 – h1)
atau dapat diubah menjadi:
p1 (m/ρ) + ½ m v21 + mgh1 = p2 (m/ρ) + ½ m v22 + mgh2
Persamaan tersebut dapat disederhanakan menjadi:
p1 + ½ ρ v21 + ρ gh1 = p2 + ½ ρ v22 + ρ gh2
atau ditulis secara umum menjadi:
p + ½ ρ v2 + ρ gh = konstan
Persamaan di atas merupakan persamaan yang menyatakan Hukum Bernoulli yang menyatakan hubungan antara kecepatan aliran dengan tinggi permukaan air dan tekanannya.
Dalam kehidupan sehari-hari Hukum Bernoulli memiliki penerapan yang beragam yang ada hubungannya dengan aliran fluida, baik aliran zat cair maupun gas. Penerapan tersebut sebagian besar dimanfaatkan dalam bidang teknik dan ilmu pengetahuan yang berkaitan dengan aliran fluida. Misalnya dalam teknologi pesawat terbang Hukum Bernoulli tersebut dimanfaatkan untuk merancang desain sayap pesawat terbang. Dalam bidang yang lain misalnya desain bentuk mobil yang hemat bahan baker, kapal laut dan sebagian alat ukur yang dapat digunakan dalam suatu peralatan pengendali kecepatan dan sebagainya.
Dengan mengusahakan bentuk sayap pesawat terbang seperti yang tergambar di bawah ini, maka bagian depan dari sayap tersebut memiliki permukaan yang tidak kaku sehingga dapat memberikan kemudahan dalam aliran udara. Lihat gambar!

Gambar 14. Penampang sayap pesawat terbang.
Bentuk sayap yang demikian sengaja dirancang agar aliran yang mengenai bagian depan dari sayap akan membentuk aliran laminier. Dari gambar di samping ini dapat dijelaskan bahwa apabila pesawat terbang digerakkan dengan ke depan kecepatan udara di bagian atas pesawat dan kecepatan udara yang lewat bagian bawah pesawat terbang akan menjadi tidak sama. Kecepatan aliran udara pada bagian atas akan cenderung lebih besar daripada kecepatan aliran udara bagian bawah pesawat terbang. Hal ini mengakibatkan munculnya gaya pengangkatan yang bekerja pada pesawat terbang sehingga pesawat terbang dapat naik ke udara.
Persamaan hidrostatika merupakan kejadian khusus dari penerapan Hukum Bernoulli bila fluida dalam keadaan diam, yakni bahwa fluida tersebut. Fluida dalam keadaan statis maka kecepatan alirannya di mana-mana akan sama dengan nol. Selanjutnya perubahan tekanan akibat letaknya titik dalam fluida yang tidak termampatkan dapat diterangkan dengan gambar sebagai berikut:

Gambar 15. Manometer.
Dari gambar dalam keadaan statis: v1 = v2 = 0
p1= po dan h1 = h2 dan h2 = 0
Berdasarkan Hukum Bernoulli p + ½ v2 = gh = konstan, dapat dituliskan menjadi
po + 0 + ρ gh = p2 + 0 + 0
p2 = po + ρ gh
Pipa venturi merupakan sebuah pipa yang memiliki penampang bagian tengahnya lebih sempit dan diletakkan mendatar dengan dilengkapi dengan pipa pengendali untuk mengetahui permukaan air yang ada sehingga besarnya tekanan dapat diperhitungkan. Dalam pipa venturi ini luas penampang pipa bagian tepi memiliki penampang yang lebih luas daripada bagian tengahnya atau diameter pipa bagian tepi lebih besar daripada bagian tengahnya. Zat cair dialirkan melalui pipa yang penampangnya lebih besar lalu akan mengalir melalui pipa yang memiliki penampang yang lebih sempit, dengan demikian maka akan terjadi perubahan kecepatan. Apabila kecepatan aliran yang melalui penampang lebih besar adalah v1 dan kecepatan aliran yang melalui pipa sempit adalah v2, maka kecepatan yang lewat pipa sempit akan memiliki laju yang lebih besar (v1 <>2). Dengan cara demikian tekanan yang ada pada bagian pipa lebih sempit akan menjadi lebih kecil daripada tekanan pada bagian pipa yang berpenampang lebih besar. Lihat gambar di bawah ini.

Gambar 16. Venturimeter
Dalam aliran seperti yang digambarkan di atas akan berlaku Hukum Bernoulli sebagai berikut:
p1 + ρ gh1 + ½ ρ v21 = p2 + ρ gh2 + ½ ρ v22
pipa dalam keadaan mendatar h1 = h2
ρ gh1 + ρ gh2
sehingga: p1 + ½ ρ v21 = p2 + ½ ρ v22
di sini v1 > v2 maka p2 <>1
akibatnya p1 – p2 = ½ ρ (v22 - v21)
padahal : p1 = pB + ρ gha
p2 = pB = ρ ghb
selanjutnya didapat:
p1 – p2 = ρ g (ha - hb)
Apabila ha - hb = h yakni selisih tinggi antara permukaan zat cair bagian kiri dan kanan, maka akan didapat:
p1 – p2 = ρ gh
Dengan mengetahui selisih tinggi permukaan zat cair pada pipa pengendalli akan dapat diketahui perubahan tekanannya yang selanjutnya perubahan kecepatan dapat juga diketahui. Oleh sebab itu pipa venturi ini akan sangat berguna untuk pengaturan aliran bensin dalam sistem pengapian pada kendaraan bermotor.
Tabung Pitot atau sering disebut pipa Pitot ini merupakan suatu peralatan yang dapat dikembangkan sebagai pengukur kecepatan gerak pesawat terbang. Melalui tabung ini umumnya dapat diketahui adalah kecepatan gerak pesawat terbang terhadap udara. Hal ini berarti apa yang terukur bukanlah kecepatan gerak terhadap kedudukan bumi. Oleh sebab itu untuk dapat mengukur kecepatan gerak pesawat terbang terhadap bumi, maka kecepatan udara harus dapat diketahui. Prinsip kerjanya tabung Pitot ini perhatikan gambar di bawah ini:

Gambar 17. Tabung/pipa Pitot
Adapun cara kerjanya dapat dikemukakan sebagai berikut: apabila alat ini digerakkan dengan cepat sekali (diletakkan dalam badan pesawat terbang) ke arah kiri sehingga udara akan bergerak dalam arah yang sebaliknya yakni menuju arah kanan. Mula-mula udara akan masuk melalui lubang pertama, selanjutnya mengisi ruang tersebut sampai penuh. Setelah udara dapat mengisi ruang tersebut melalui lubang pertama dengan penuh maka udara tersebut akan dalam keadaan diam. Udara yang lewat lubang kedua akan selalu mengalir dan kecepatan udara yang mengalir melalui lubang pertama jauh lebih kecil daripada kecepatan pengaliran udaran yang melalui lubang kedua. Oleh sebab itu dapat dianggap v1 = 0 dan perbedaan tekanan diketahui dari perbedaan tinggi permukaan air raksa dalam pipa U. Untuk memudahkan perhitungan dalam keadaan mendatar maka tidak terdapat selisih tinggi hingga akan berlaku h1 = h2 dan Hukum Bernoulli dapat ditulis menjadi:
p1 + ½ ρ v21 = p2 + ½ ρ v22
v1 = 0, maka
p1 = p2 + ½ ρ v22 untuk v2 = v

 maka p1 - p2 = ½ ρ v2
maka p1 - p2 = ½ ρ v2
 2 (p1 - p2)
2 (p1 - p2)
 atau v =
atau v =
ρ
Selisih tekanan dapat diketahui dengan mengukur perbedaan tinggi air raksa dalam pipa U tersebut maka kecepatan gerak pesawat terbang terhadap udara dapat diketahui dan dihitung dengan persamaan tersbeut.
Untuk menurunkan tekanan dalam suatu ruangan tertentu dapat dipergunakan pompa penghisap udara yang bekerja berdasarkan Hukum Bernoulli. Prinsip kerjanya dapat dilukiskan dalam gambar sebagai berikut:

Gambar 18. Prinsip kerja pipa penghisap udara.
Andaikan udara dalam ruangan R akan dikurangi atau dihisap melalui pompa penghisap yang bekerja berdasarkan Hukum Bernoulli maka dapat dilakukan dengan mengalirkan udara melalui pipa sempit A udara disemprotkan dengan kecepatan sangat besar (v) selanjutnya akibat aliran udara yang keluar dari pipa A tersebut maka tekanan udara yang berada pada tabung B akan menjadi semakin kecil. Hal ini mengakibatkan terjadinya perbedaan tekanan. Udara tersebut pada akhirnya akan keluar melalui lubang C secara terus-menerus. Selanjutnya dengan menyemprotkan yang berulang dan diperbesar kecepatan alirannya maka udara pada tabung R akan dapat berkurang terus-menerus sesuai dengan yang dikehendaki. Prinsip inilah yang merupakan prinsip kerja dari pompa penghisap.
Untuk dapat memahami kegiatan belajar 3 ini, jawablah pertanyaan berikut ini dengan sebaik-baiknya.
1. Dua buah bola pingpong yang digantungkan dengan seutas benang dan diletakkan berdekatan satu sama lain, selanjutnya hembuskan udara yang berada di antara dua bola pingpong tersebut. Apa yang terjadi? Jelaskan mengapa hal tersebut dapat terjadi!
2. Dengan penalaran yang sama seperti soal nomor 1, tetapi gejalanya terjadi pada zat cair, yakni bahwa kapal yang sedang berlayar akan dapat berbenturan apabila kecepatan aliran air di antara kedua kapal tersebut sangat besar. Mengapa terjadi gejala yang demikian ini?
3. Rancanglah suatu percobaan untuk memperagakan terjadinya gejala yang menunjukkan Hukum Bernoulli. Jelaskan cara kerja yang dapat dilakukan!
4. Buktikan bahwa pada aliran dari lubang melalui sebuah lubang yang digambarkan di bawah ini besarnya debit air dapat dinyatakan dengan persamaan.

Gambar 19.
5. Jelaskan prinsip kerja penyemprot hama tanaman yang digambarkan seperti gambar berikut ini dengan Hukum Bernoulli!

Gambar 20.
Kunci Jawaban latihan 3
1. Lihat gambar di bawah ini.

Gambar 21.
Dengan ditiupnya udara di antara dua bola pingpong tersebut kedua bola pingpong akan bergerak saling mendekati dan pada akhirnya keduanya dapat berbenturan satu sama lain. Terjadinya benturan antara kedua bola ini disebabkan oleh hembusan terhadap udara di antara kedua bola tersebut.
Dengan hembusan yang diberikan maka akan terdapat aliran udara di antara dua bola tersebut, akibatnya tekanan untuk daerah tersebut menjadi berkurang dan menjadi lebih kecil daripada tekanan di sekelilingnya sehingga bola pingpong terdorong untuk bergerak pada daerah yang memiliki tekanan yang lebih rendah. Selanjutnya kedua bola tersebut bergerak dalam arah yang berlawanan dan akhirnya dapat berbenturan satu sama lain.
2. Perhatikan gambar di bawah ini.
Gambar 22.
Gambar berikut merupakan dua kapal yang sedang bergerak. Terjadinya benturan antara kedua kapal tersbeut akibat aliran air yang berada di antara keuda kapal tersebut memiliki kecepatan aliran yang jauh lebih besar daripada aliran air di sekitarnya. Akibatnya tekanan air di antara dua kapal tersebut mengalami penurunan yang cukup besar yang mengakibatkan kapal bergeser dalam arah ayang berlawanan yang akibatnya dapat berbenturannya dua kapal tersebut.
3. Lihat gambar di bawah ini.

Gambar 23.
Keterangan gambar:
1) Pipa dengan diameter bagian tengah lebih sempit daripada bagian tepinya
2) Pipa pengontrol permukaan air berwarna/tinta
3) Tabung gelas yang berisi air berwarna/tinta
Dari gambar yang telah disajikan di bagian depan apabila pipa kaca yang memiliki penampang berbeda dan pipa pengendali tersbeut dicelupkan dalam air berwarna maka setting percobaan dapat disajikan dalam gambar tersebut.
Adapun langkah percobaan yang dapat dilakukan adalah:
a. Pipa pengendali dicelupkan dalam air berwarna dan tabung belum dihembuskan udara, maka permukaan air berwarna di bagian dalam dan bagian luar akan sama tinggi karena tekanan di sekelilingnya akan sama.
b. Selanjutnya pipa bagian kanan dihembus kuat-kuat, sehingga pada pipa akan terjadi aliran udara. Akibatnya berdasarkan Hukum Bernoulli tekanan pada bagian dalam tabung akan berkurang sehingga ada sebagian air berwarna dapat naik dalam pipa pengendali tersebut, yang menyebabkan perbedaan tekanan di dalam pipa dan di luar pipa. Dengan mengukur perbedaan tinggi air berwarna dan mengetahui massa jenis air berwarna maka perbedaam tekanan dapat diketahui.
4. Lihat gambar di bawah ini.

Gambar 24.
Gambar berikut memperlihatkan suatu bejana yang pada bagian bawah diberikan lubang yang sempit untuk pengeluaran air (peluahan air). Jarak lubang tersebut pada awal percobaan adalah h cm dari permukaan air yang diisikan ke dalam bejana tersebut. Apabila tekanan mula-mula dari udara di sekeliling pipa adalah PB dan lubang peluahan air disebut lubang R, serta tinggi permukaan air mula-mula adalah p, maka setelah lubang sempit tersebut dibiarkan terbuka maka air yang meluah melalui lubang R tersebut akan memancar keluar. Oleh karena lubang R tersebut relatif kecil bila dibandingkan dengan diameter bejana, maka gerak permukaan air dalam bejana (P) tersebut amat lambat, berarti vp sangat kecil atau dapat disamakan dengan nol. Selanjutnya berdasarkan Hukum Bernoulli, akan dapat dituliskan sebagai berikut:
p1 + ρ gh1 + ½ ρ v21 = p2 + ρ gh2 + ½ ρ v22
Apabila lubang R sebagai lubang referensi maka dapat dikemukakan bahwa
v1 = 0, h2 = 0 dan p1 = p2 dan v2 = v
maka Hukum Bernoulli dapat dituliskan menjadi
pB + ρ gh + pB + ½ ρ v2
atau
½ ρ v2 = ρ gh
V = √2 gh
Apabila luas penampang lubang diberikan notasi A maka besarnya debit
(Q) = A √2 gh
5. Perhatikan gambar di bawah ini.

Gambar 25.
Keterangan gambar:
1) Lubang kecil berada di ujung penyemprot
2) Penghisap yang dapat bergerak bebas tanpa gesekan
3) Tabung penyemprot yang diisi dengan cairan obat hama
Prinsip bekerjanya alat tersebut dapat didasarkan pada Hukum Bernoulli yang dapat dinyatakan sebagai berikut:
p + ρ gh + ½ ρ v2 = konstan
Penghisap ditekan dalam keadaan mendatar berartiakan berlaku
ρ gh1 = ρ gh2, sehingga persamaan tersebut dapat dituliskan menjadi
p1 + ½ ρ v21 = p2 + ½ ρ v22
p1 - p2 = ½ ρ (v22 - v21)
Jika p1 <>1 > v2, jadi pada tempat yang tekanannya kecil maka kecepatan pengalirannya akan besar.
Rangkuman
Hukum Bernoulli merupakan salah satu dasar yang perlu dipahami dalam menjelaskan aliran fluida terutama fluida tanpa kekentalan. Hal ini memberikan gambaran bahwa Hukum Bernoulli dapat menerangkan gejala lairan fluida yang laminier atau bahkan fluida ideal. Banyak penerapan yang berkaitan dengan Hukum Bernoulli tersebut terutama berkaitan dengan desain peralatan yang hemat energi seperti diungkapkan di bagian depan.
Tes Formatif 3
Jawablah soal berikut ini dengan memilih salah satu jawaban yang benar dengan memberikan tanda silang pada huruf (A), (B), (C), atau (D) di lembar jawaban yang disediakan!
1. Air mengalir melalui penampang pipa yang memiliki luas penampang yang berbeda, yakni pada bagian ujung kiri memiliki luas penampang lebih besar daripada penampang bagian kanan. Pada pipa yang memiliki penampang lebih kecil ternyata air mengalir lebih cepat daripada air yang mengalir melalui pipa yang memiliki penampang lebih besar. Dalam keadaan demikian maka akan berlaku:
A. A1 V1 > A2 V2
B. A1 V1 <>2 V2
C. A1 V1 = A2 V2
D. A1 V1 <>2 V2
2. Tersedia 4 mesin pompa air di musim kemarau, mesin A, mesin B, mesin C, dan mesin D secara berurutan memiliki debit 1,5 liter/sec, 2 liter/sec, 4 liter/sec, dan 5 liter/sec. Agar sawah seluas 1 hektar dapat dialiri secara merata selama 7 jam dengan ketebalan oncoran rata-rata 1 cm maka pompa yang dapat digunakan minimal adalah pompa……
A. A
B. B
C. C
D. D
3. Penyemprot hama tanaman digunakan para petani untuk pemberantas hama di suatu tempat. Agar didapat efisiensi yang lebih tinggi maka bagian ujung pipa yang memancarkan cairan obat perlu dibuat lubang yang memiliki penampang jauh lebih kecil daripada bagian ujung yang dekat dengan reservoir cairan obatnya. Prinsip pembuatan tersebut didasarkan pada huum Bernoulli dengan pertimbangan bahwa……
A. Pada bagian ujung tempat keluarnya cairan pembasmi hama akan memiliki kecepatan pengaliran yang lebih besar karena tekanannya besar
B. Bagian ujung tempat keluarnya cairan pembasmi memiliki kecepatan yang besar karena tekanannya kecil
C. Bagian ujung tempat keluarnya cairan pembasmi memiliki kecepatan yang kecil karena tekanannya besar
D. Bagian ujung tempat keluarnya cairan pembasmi memiliki kecepatan yang kecil karena tekanannya kecil
4. Lihat gambar di bawah ini. Zat cair dalam bejana A yang berada di atas dari bejana lain B diisi zat cair dan zat cair akan dipindahkan dari bejana A ke bejana B. Pipa pemindah memiliki luas penampang yang sama dan dipindahkan dengan cara seperti digambarkan berikut ini. Apabila massa jenis zat cair adalah 1,25 gr/cc dan tekanan udara di sekeliling pipa adalah 76 cm Hg dan percepatan gravitasi bumi di tempat tersebut adalah 10 m/sec2, maka agar pemindahan dapat dilaksanakan tanpa bantuan tenaga dari luar panjangnya pipa p ke Q adalah…..

A. 0
B. 4 cm
C. 8 cm
D. Jawaban A, B, dan C salah
5. Lihat gambar di bawah ini. Suatu bejana yang memiliki permukaan yang lebar dialirkan melalui lubang kecil yang diameternya 2 cm2 dan tinggi permukaan air dalam tabung tersebut adalah 125 cm dihitung dari lubang peluahan air tersebut. Apabila percepatan gravitasi di tempat tersebut adalah 10 m/sec2, maka besarnya debit air yang dapat keluar melewati lubang tersebut adalah…….

A. 1000 cc/sec
B. 500 cc/sec
C. 100 cc/sec
D. 50 cc/sec
6. Lihat gambar di bawah ini! Suatu pipa yang bentuknya seperti digambarkan berikut ini dialiri air melalui titik P dan Q tersebut adalah 125 cm di atas lantai mendatar. Apabila diameter pipa pada P adalah 20 cm dan Q adalah 10 cm, maka air yang jatuh di lantai mencapai jarak mendatar sejauh 200 cm (lihat gambar). Apabila percepatan gravitasi bumi di tempat itu adalah 10 m/sec2, maka besarnya kecepatan aliran pada ujung P adalah………

A. 1 m/sec
B. 15 m/sec
C. 2 m/sec
D. 25 m/sec
7. Sebuah tabung Pitot seperti gambar di bawah ini delengkapi dengan manometer digunakan untuk mengukur kecepatan pengaliran gas dalam suatu pipa. Apabila massa jenis gas dalam pipa tersebut adalah 0,0136 gr/cc dan massa jenis air raksa dalam manometer adalah 13,6 gr/cc percepatan gravitasi bumi di tempat itu adalah 10 m/sec2. Pada saat pengukuran dilakukan selisih tinggi permukaan air raksa dalam manometer tersebut adalah 2 cm. Besarnya kecepatan arus pengaliran gas dalam tabung pipa tersebut adalah……

A. 20 m/sec
B. 25 m/sec
C. 30 m/sec
D. 40 m/sec
8. Lihat gambar di bawah ini. Suatu bak tendon air berbentuk silinder memiliki luas penampang yang luas dan berisi air penuh. Tinggi silinder tersebut adalah 145 cm dan pada ketinggian 125 cm dari dasar bak dibuat luas yang sempit untuk mengalirkan air. Anggaplah percepatan gravitasi bumi 10 m/sec2 maka besarnya laju air yang melalui lubang tersebut adalah……

A. 1 m/sec
B. 2 m/sec
C. 3 m/sec
D. 4 m/sec
9. Seperti soal nomor 8 di bagian depan, gunakan ketentuan yang ada pada nomor tersebut, besarnya jarak pancaran pertama kali yang jatuh ke permukaan lantai bila diukur dari dinding silinder secara mendatar pada lantai tersebut adalah…..
A. 50 cm
B. 75 cm
C. 100 cm
D. 125 cm
10. Suatu zat cair A volumenya 80 cc dan massa jenisnya 0,92 gr/cc dicampur dengan zat cair lain B yang volumenya 120 cc dengan massa jenis 0,62 gr/cc. Apabila dalam pencampuran tersebut diandaikan tidak terjadi perubahan volume mnaka massa jenis zat cair campuran tersebut adalah…..
A. 0,84 gr/cc
B. 0,81 gr/cc
C. 0,76 gr/cc
D. 0,74 gr/cc
Cocokkanlah jawaban Anda dengan kunci jawaban tes formatif 3 yang ada di bagian akhir modul ini. Hitunglah jumlah jawaban Anda yang benar, kemudian gunakan di bawah ini untuk mengetahui tingkat penguasaan Anda terhadap materi di atas.
Rumus:
Tingkat penguasaan = Jumlah jawaban Anda yang benar = 100 %
10
Arti tingkat penguasaan yang Anda capai:
90 % - 100 % = baik sekali
80 % - 89 % = baik
70 % - 79% = cukup
< style=""> = kurang
Kalau Anda mencapai tingkatan penguasaan 80 % atau lebih, Anda dapat meneruskan dengan modul berikutnya. Tetapi kalau kurang dari 80 % Anda harus mengulangi kegiatan belajar ini, terutama bagian yang belum Anda kuasai.
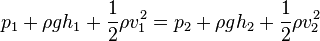





![]() dan
dan



![]() dan
dan



![]() dan
dan




















